
Υλοποίηση αυτομάτων με την κλάση DFA¶
Στα παραδείγματα και τις ασκήσεις θα χρησιμοποιήσουμε την έτοιμη κλάση DFA από τη βιβλιοθήκη compilerlabs. Η κλάση αυτή παρέχει ένα απλό interface για την κατασκευή και λειτουργία αυτομάτων DFA.
Κατασκευή και χρήση αυτομάτου DFA¶
Αρχικά κάνουμε import την κλάση DFA στο πρόγραμμά μας:
from compilerlabs import DFA
Αμέσως μετά δημιουργούμε ένα αυτόματο, στιγμιότυπο της κλάσης DFA:
test_dfa = DFA('s0')
Το υποχρεωτικό όρισμα στην DFA() είναι το όνομα της αρχικής κατάστασης του αυτομάτου (εδώ s0).
Στη συνέχεια, μπορούμε να ορίσουμε μεταβάσεις του αυτομάτου μέσω της μεθόδου transition(fromstate,next_input,tostate) όπου fromstate είναι η κατάσταση απ’ όπου, με την εμφάνιση του χαρακτήρα next_input, μεταβαίνουμε στη νέα κατάσταση tostate, π.χ.:
test_dfa.transition('s0','t','s1')
που σημαίνει ότι όταν βρισκόμαστε στην κατάσταση s0 και εμφανιστεί ο χαρακτήρας t θα μεταβούμε στην κατάσταση s1.
Μπορούμε ακόμα να δώσουμε μια λίστα χαρακτήρων για μετάβαση, π.χ.
test_dfa.transition('s1',['0','1','2'],'s2')
που δηλώνει μετάβαση από το s1 στο s2 με έναν οποιονδήποτε χαρακτήρα από τους 0, 1 ή 2. Προσέξτε ότι το προηγούμενο είναι ισοδύναμο με το:
test_dfa.transition('s1','0','s2')
test_dfa.transition('s1','1','s2')
test_dfa.transition('s1','2','s2')
Η χρήση της μεθόδου accept(state,token) είναι αυτή που ορίζει μια κατάσταση ως κατάσταση αποδοχής. Μέσω της accept ορίζουμε το σύμβολο (token) που επιστρέφεται:
test_dfa.accept('s2','TOK1')
Στο προηγούμενο παράδειγμα η s2 ορίζεται ως κατάσταση αποδοχής που αναγνωρίζει και επιστρέφει το σύμβολο TOK1.
Όταν ολοκληρώσουμε τον ορισμό των μεταβάσεων και τις καταστάσεις αποδοχής του αυτομάτου, μπορούμε να το χρησιμοποιήσουμε για να ελέγξουμε ταιριάσματα σε strings. Η μέθοδος που παρέχεται ονομάζεται scan(text), όπου text είναι το string που θα προσπαθήσουμε να ταιριάξουμε:
token,lexeme = test_dfa.scan('t2')
Η μέθοδος επιστρέφει το token που αναγνωρίστηκε (ή None αν δεν υπάρχει ταίριασμα) και το αντίστοιχο κείμενο (ή το κενό string αν δεν αναγνωρίστηκε κάτι).
Παράδειγμα: το αυτόματο για τα long, term και test¶
Στη συνέχεια θα δούμε την υλοποίηση του γνωστού παραδείγματος του αυτομάτου με τα τρία keywords, τις λέξεις long, term και test του επόμενου σχήματος:
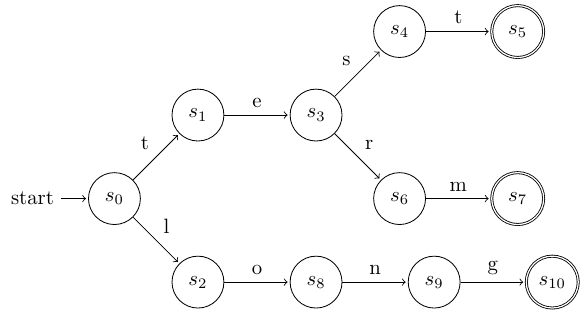
Το αυτόματο πεπερασμένων καταστάσεων για τα keywords long, term, test¶
Η υλοποίηση μέσω της κλάσης DFA:
from compilerlabs import DFA
dfa1 = DFA('s0')
dfa1.transition('s0','t','s1')
dfa1.transition('s0','l','s2')
dfa1.transition('s1','e','s3')
dfa1.transition('s3','s','s4')
dfa1.transition('s4','t','s5')
dfa1.transition('s3','r','s6')
dfa1.transition('s6','m','s7')
dfa1.transition('s2','o','s8')
dfa1.transition('s8','n','s9')
dfa1.transition('s9','g','s10')
dfa1.accept('s5','TEST_TOKEN')
dfa1.accept('s7','TERM_TOKEN')
dfa1.accept('s10','LONG_TOKEN')
token,lexeme = dfa1.scan('long')
print(token,lexeme) # prints LONG_TOKEN long
token,lexeme = dfa1.scan('term')
print(token,lexeme) # prints TERM_TOKEN term
token,lexeme = dfa1.scan('test')
print(token,lexeme) # prints TEST_TOKEN test
Παράδειγμα: το αυτόματο για τον αριθμό μήνα (1..12)¶
Το αυτόματο για την αναγνώριση αριθμών μήνα (1..12) με ένα ή δύο ψηφία έχει παρουσιαστεί σε προηγούμενη ενότητα και είναι ως εξής:
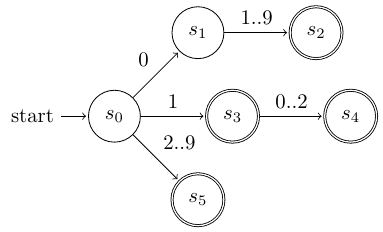
Αυτόματο πεπερασμένων καταστάσεων για αναγνώριση αριθμού μήνα¶
Πώς θα υλοποιηθεί με την κλάση DFA;
Δείτε τη λύση
from compilerlabs import DFA
dfa = DFA('s0')
dfa.transition('s0','0','s1')
dfa.transition('s1',['1','2','3','4','5','6','7','8','9'],'s2')
dfa.transition('s0','1','s3')
dfa.transition('s3',['0','1','2'],'s4')
dfa.transition('s0',['2','3','4','5','6','7','8','9'],'s5')
dfa.accept('s2','MONTH')
dfa.accept('s3','MONTH')
dfa.accept('s4','MONTH')
dfa.accept('s5','MONTH')
for s in ['3','02','12','0','00','15','32','1']:
token,lexeme = dfa.scan(s)
print(s,token,lexeme)
Η εκτέλεση του κώδικα θα δώσει ως έξοδο (αριστερά είναι η είσοδος, στο κέντρο το token που αναγνωρίστηκε και δεξιά το μέρος της εισόδου που καταναλώθηκε):
3 MONTH 3
02 MONTH 02
12 MONTH 12
0 None
00 None
15 MONTH 1
32 MONTH 3
1 MONTH 1
Ομαδοποίηση χαρακτήρων¶
Ας εξετάσουμε την υλοποίηση του αυτομάτου DFA το οποίο αναγνωρίζει ακολουθίες ψηφίων 0..9 οποιουδήποτε μήκους:

Αυτόματο πεπερασμένων καταστάσεων για αναγνώριση σειράς ψηφίων¶
Για να περιγράψουμε τη μετάβαση από το \(s_0\) στο \(s_1\) θα μπορούσαμε να γράψουμε:
num_dfa.transition('s0',['0','1','2','3','4','5','6','7','8','9',],'s1')
Για να διευκολύνει την κατασκευή, το interface της κλάσης DFA επιτρέπει την προαιρετική χρήση ενός «προ-επεξεργαστή» (preprocessor) των χαρακτήρων εισόδου, ο οποίος μπορεί να ομαδοποιήσει διάφορους χαρακτήρες σε μια και μόνο αναγνωριστική ετικέτα. Στο παράδειγμα του αυτομάτου των αριθμητικών ψηφίων μπορούμε να ορίσουμε:
def preproc(c):
if c>='0' and c<='9':
return 'DIGIT'
return c
Το όνομα της συνάρτησης του preprocessor περνάει ως δεύτερο προαιρετικό όρισμα στην κατασκευή του DFA:
dfa2 = DFA('s0',preproc)
Έχοντας ορίσει τον preprocessor της εισόδου όπως πριν, το αυτόματο μπορεί να κατασκευαστεί ως εξής:
dfa2.transition('s0','DIGIT','s1')
dfa2.transition('s1','DIGIT','s1')
dfa2.accept('s1','NUMBER_TOKEN')
Παράδειγμα αναζήτησης:
token,lexeme = dfa2.scan('123')
print(token,lexeme) # prints NUMBER_TOKEN 123
Διαφορές από το θεωρητικό αυτόματο¶
Το θεωρητικό αυτόματο (D)FA θα προσπαθήσει να ταιριάξει όλους τους χαρακτήρες εισόδου. Εάν για κάποιον χαρακτήρα δεν υπάρχει μετάβαση από την τρέχουσα κατάσταση θα παραχθεί σφάλμα. Το θεωρητικό αυτόματο αναγνωρίζει ένα κείμενο όταν, αφού το καταναλώσει όλο, βρίσκεται σε κατάσταση αποδοχής.

Αυτόματο πεπερασμένων καταστάσεων για αναγνώριση σειράς ψηφίων¶
Για παράδειγμα, το θεωρητικό αυτόματο που αναγνωρίζει σειρές από αριθμητικά ψηφία (0..9) στο προηγούμενο σχήμα θα επιστρέψει σφάλμα τόσο στο a123 (επειδή από την αρχική κατάσταση δεν υπάρχει μετάβαση με τον χαρακτήρα a) όσο και στο 123a (γιατί από το s1 δεν υπάρχει μετάβαση με το a).
Η λειτουργία του θεωρητικού αυτομάτου εξυπηρετεί πρακτικά μόνο αν θέλουμε να ελέγξουμε την εγκυρότητα όλου του κειμένου εισόδου (input validation).
Υπάρχουν όμως και άλλες πιθανές πρακτικές χρήσεις ενός αυτομάτου, όπως:
Αναζήτηση (search): εδώ ψάχνουμε για την εμφάνιση ενός σχεδίου κειμένου μέσα σε ένα μεγαλύτερο κείμενο. Π.χ. στην είσοδο
123aθα θέλαμε να αναγνωρίσουμε το123μόνο.Μετατροπή σε σύμβολα (tokenization): η κλασσική λειτουργία στο πρώτο βήμα ενός μεταγλωττιστή, όπου επαναληπτικά αναγνωρίζουμε σχέδια κειμένου σε ένα μεγαλύτερο κείμενο. Π.χ. από το
int k;να αναγνωρίσουμε τα σύμβολα (tokens)KEYWORD_INT,SPACE,IDENTIFIERκαιSEMICOLON.
Για να επιτρέψει την υλοποίηση των παραπάνω, το αυτόματο της κλάσης DFA που χρησιμοποιούμε στο εργαστήριο λειτουργεί ως εξής:
Εάν δεν είναι δυνατή η μετάβαση από την τρέχουσα κατάσταση με τον χαρακτήρα εισόδου, ελέγχεται εάν η κατάσταση αυτή είναι κατάσταση αποδοχής.
Εάν ναι, τότε αναγνωρίζεται το κείμενο μέχρι το σημείο αυτό (μέρος δηλαδή του συνολικού κειμένου).
Εάν όχι, παράγεται σφάλμα.
Στο παράδειγμα του αυτομάτου των αριθμητικών ψηφίων, η κλάση DFA θα αναγνωρίσει με επιτυχία το μέρος 123 της εισόδου 123a.
Προαιρετικά ταιριάσματα¶
Έστω ότι υλοποιείται το αυτόματο της επόμενης εικόνας:

Αυτόματο για την αναγνώριση int και float αριθμών¶
Ο στόχος είναι η αναγνώριση ακεραίων αριθμών (στην κατάσταση \(s_1\)) και αριθμών με δεκαδικό μέρος (στην κατάσταση αποδοχής \(s_3\)).
Εάν το string εισόδου είναι το '123.', θα θέλαμε να αναγνωρίσουμε το 123 ως ακέραιο. Κάτι τέτοιο δεν θα συμβεί όμως κανονικά, γιατί στο τέλος της αναζήτησης βρισκόμαστε στην κατάσταση \(s_2\), η οποία δεν είναι κατάσταση αποδοχής.
Για να διορθωθεί αυτή η ατέλεια έχει εισαχθεί στη scan() η δυνατότητα μνήμης, όπου φυλάσσεται η τελευταία κατάσταση αποδοχής όπου έχει βρεθεί το αυτόματο. Αυτή η κατάσταση (αν υπάρχει) επιστρέφεται όταν δεν μπορούμε να προχωρήσουμε άλλο.
Το αυτόματο για την αναγνώριση int και float αριθμών μπορεί να υλοποιηθεί με την κλάση DFA ως εξής:
def preproc(c):
if c>='0' and c<='9':
return 'DIGIT'
return c
dfa3 = DFA('s0',preproc)
dfa3.transition('s0','DIGIT','s1')
dfa3.transition('s1','DIGIT','s1')
dfa3.transition('s1','.','s2')
dfa3.transition('s2','DIGIT','s3')
dfa3.transition('s3','DIGIT','s3')
dfa3.accept('s1','INT_TOKEN')
dfa3.accept('s3','FLOAT_TOKEN')
token,lexeme = dfa3.scan('123')
print(token,lexeme) # prints INT_TOKEN 123
token,lexeme = dfa3.scan('123.')
print(token,lexeme) # prints INT_TOKEN 123
token,lexeme = dfa3.scan('123.4')
print(token,lexeme) # prints FLOAT_TOKEN 123.4
Ασκήσεις¶
Υλοποιήστε μέσω της κλάσης
DFAαυτόματο για την αναγνώριση ακέραιων και δεκαδικών αριθμών οποιουδήποτε μήκους στις εξής μορφές:
1234(επιστρεφόμενο σύμβολο:INT_TOKEN)
123.48(επιστρεφόμενο σύμβολο:FLOAT_TOKEN)
123.48e56(επιστρεφόμενο σύμβολο:SCIENTIFIC_TOKEN)
Υλοποιήστε μέσω μέσω της κλάσης
DFAαυτόματο για την αναγνώριση έγκυρων μορφών 24ωρης ώρας (00:00έως23:59).
Η ώρα μπορεί να εκφράζεται με ένα ή δύο ψηφία (π.χ.
3:45αλλά και03:45).Τα λεπτά θα έχουν πάντα δύο ψηφία.
Κάθε άκυρη μορφή ώρας δεν πρέπει να αναγνωρίζεται (π.χ.
31:13ή9:72).
Υλοποιήστε μέσω μέσω της κλάσης
DFAαυτόματο για την αναγνώριση αριθμών μητρώου φοιτητών στη μορφήΠ2013000για τα έτη 2004 έως 2020.
Προηγείται το γράμμα
Π.Ακολουθεί το έτος με τέσσερα ψηφία (2004 έως και 2020).
Στο τέλος είναι ο αριθμός του φοιτητή με τρία ψηφία.
