
Εισαγωγή στη λεκτική ανάλυση¶
Στην ενότητα αυτή εξετάζουμε το πρώτο στάδιο ενός μεταγλωττιστή, τη λεκτική ανάλυση, η οποία μετατρέπει τον πηγαίο κώδικα (source files) σε σύμβολα (tokens). Το στάδιο αυτό μπορεί να ειδωθεί ως μια μορφή προ-επεξεργασίας (preprocessing), πριν την περισσότερο απαιτητική υπολογιστικά συντακτική ανάλυση.
Η λειτουργία της λεκτικής ανάλυσης¶
Η λεκτική ανάλυση (lexical analysis, lexing ή scanning) δέχεται ως είσοδο έναν-έναν τους μεμονωμένους χαρακτήρες του πηγαίου κώδικα και παράγει σύμβολα (tokens). Δείτε το επόμενο σχήμα:

Παράδειγμα λεκτικής ανάλυσης¶
Στην είσοδο έχουμε τους μεμονωμένους χαρακτήρες "int k;". Η λεκτική ανάλυση τους ομαδοποιεί στα σύμβολα KEYWORD_INT, SPACE, IDENTIFIER και SEMICOLON. Παρατηρείστε ότι:
Ένα σύμβολο (token) συνοδεύεται πάντοτε από το κείμενο που του αντιστοιχεί (lexeme).
Για τα
KEYWORD_INTήSEMICOLONξέρουμε πάντοτε ποιο κείμενο αντιστοιχεί ("int"και";"), συνεπώς το lexeme δεν μας ενδιαφέρει.Αντιθέτως, για το token
IDENTIFIER(ονόματα μεταβλητών κλπ) η πληροφορία του lexeme ("k") είναι σημαντική για τον μεταγλωττιστή.
Ο λεκτικός αναλυτής συνήθως «καθαρίζει» την είσοδο, π.χ. απορρίπτοντας σχόλια ή τα κενά (spaces) σε γλώσσες όπως η C. Αυτό βέβαια εξαρτάται από τη γλώσσα προγραμματισμού: για την Python π.χ., τα κενά της στοίχισης δεν πρέπει να απορριφθούν.
Όπως είναι φανερό από τα προηγούμενα, χρειαζόμαστε έναν μηχανισμό για την αναγνώριση συγκεκριμένων πρότυπων σχεδίων κειμένου (text patterns). Ο μηχανισμός αυτός βασίζεται στη θεωρία των αυτομάτων πεπερασμένων καταστάσεων, τα οποία αναλύονται στη συνέχεια.
Αυτόματα πεπερασμένων καταστάσεων¶
Από τη «Θεωρία Υπολογισμού»: Κάθε αυτόματο πεπερασμένων καταστάσεων (finite automaton –FA) είναι μια πεντάδα \((Q, \Sigma, \delta, q_0, F)\), όπου
\(Q\) ένα πεπερασμένο σύνολο καταστάσεων
συν μια κατάσταση σφάλματος \(q_e\)
\(\Sigma\) ένα πεπερασμένο αλφάβητο
σύνολο χαρακτήρων εισόδου
\(\delta \colon Q \times \Sigma \to Q\) η συνάρτηση μετάβασης
από την τρέχουσα στην επόμενη κατάσταση, με την εμφάνιση ενός νέου χαρακτήρα εισόδου
αν δεν υπάρχει μετάβαση, τότε σφάλμα
\(q_0 \in Q\) η αρχική κατάσταση
\(F \subseteq Q\) το σύνολο των καταστάσεων αποδοχής
εάν βρισκόμαστε σε κατάσταση αποδοχής όταν τελειώσει η ανάλυση, τότε αποδεχόμαστε το κείμενο εισόδου
Σε μια τυπική εφαρμογή μεταγλωττιστή, το αλφάβητο \(\Sigma\) είναι όλοι οι χαρακτήρες που αναγνωρίζει η γλώσσα προγραμματισμού.
Χρήση στη λεκτική ανάλυση¶
Πώς χρησιμοποιείται πρακτικά το αυτόματο FA στη λεκτική ανάλυση; Ο στόχος είναι να αναγνωρίσουμε συγκεκριμένες ακολουθίες (patterns) χαρακτήρων εισόδου. Κατά τη διαδικασία της αναγνώρισης θέλουμε να ξέρουμε σε κάθε στιγμή:
Ποιους χαρακτήρες έχουμε ήδη αναγνωρίσει έως τώρα;
Στο σημείο που βρισκόμαστε, ποιοι είναι οι επόμενοι έγκυροι χαρακτήρες;
Αυτό μπορεί να γίνει με τη βοήθεια ενός αυτομάτου. Δείτε την εικόνα που ακολουθεί:
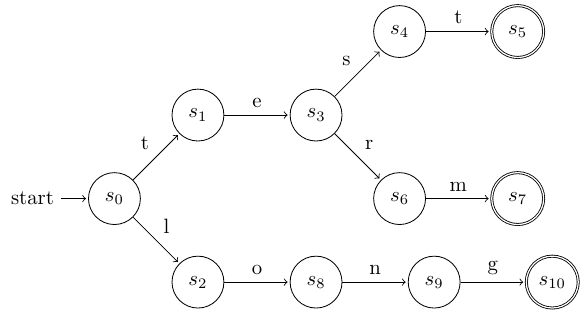
Αυτόματο πεπερασμένων καταστάσεων για τα keywords long, term, test¶
Το αυτόματο αυτό είναι σχεδιασμένο για να αναγνωρίζει τρία keywords, τις λέξεις long, term και test.
Στην αρχή της διαδικασίας βρισκόμαστε στην αρχική κατάσταση \(s_0\).
Εάν ο πρώτος χαρακτήρας εισόδου είναι το t μεταβαίνουμε στην κατάσταση \(s_1\), αν είναι το l, στην \(s_2\). Για κάθε άλλο χαρακτήρα εισόδου δεν προβλέπεται μετάβαση, συνεπώς μεταβαίνουμε σε κατάσταση σφάλματος.
Όντας στις καταστάσεις \(s_1\) ή \(s_2\), διαβάζουμε τον επόμενο χαρακτήρα εισόδου και προχωράμε σε επόμενη κατάσταση αν αυτό είναι δυνατό.
Η διαδικασία επαναλαμβάνεται όσο δεν υπάρχει σφάλμα και όσο υπάρχουν επόμενοι χαρακτήρες εισόδου.
Όταν εξαντληθεί η είσοδος, ελέγχουμε αν βρισκόμαστε σε κατάσταση αποδοχής.
Αν όχι, δεν έχουμε αναγνωρίσει πλήρως κάτι από τα ζητούμενα, οπότε επιστρέφεται σφάλμα.
Αν ναι, έχουμε αναγνωρίσει το κείμενο που αντιστοιχεί στην κατάσταση που βρισκόμαστε (π.χ. αν είμαστε στην κατάσταση \(s_7\) έχουμε αναγνωρίσει τη λέξη term.
Συνοψίζοντας, η τρέχουσα κατάσταση του αυτομάτου προσδιορίζει σε ποιο σημείο της διαδικασίας αναγνώρισης βρισκόμαστε και ποιοι χαρακτήρες επιτρέπεται να ακολουθήσουν.
Παράδειγμα: αναγνώριση αριθμού μήνα (1..12)¶
Θέλουμε να κατασκευάσουμε ένα αυτόματο που να αναγνωρίζει αριθμούς μηνών, δηλαδή τους αριθμούς 1 έως και 12. Οι αριθμοί 1 έως 9 θα πρέπει να αναγνωρίζονται με ένα ψηφίο (1..9) ή με δύο (01..09). Το σημαντικό είναι να παρατηρήσουμε ότι σε κάθε μετάβαση του αυτομάτου καταναλώνουμε έναν μόνο χαρακτήρα. Για παράδειγμα, στην αναγνώριση του 12 θα γίνουν δύο μεταβάσεις: η πρώτη με τον χαρακτήρα 1 και η δεύτερη με τον χαρακτήρα 2.
Δείτε τη λύση
Η αναγνώριση δίνεται από το αυτόματο που ακολουθεί. Παρατηρήστε ότι γίνεται με διαφορετικό τρόπο η αναγνώριση, ανάλογα με το πρώτο ψηφίο του αριθμού:
Αν το πρώτο ψηφίο είναι 0, πρέπει να ακολουθεί ένα δεύτερο ψηφίο από το 1 έως και το 9. Αυτό αναγνωρίζει τους αριθμούς με δύο ψηφία
00..09.Αν το πρώτο ψηφίο είναι 1, πιθανόν να έχουμε αναγνωρίσει το
1. Το αυτόματο όμως θα εξετάσει και τον επόμενο χαρακτήρα, μήπως πρόκειται για τους αριθμούς10..12.Τέλος, αν το πρώτο ψηφίο είναι ένα από τα
2..9, έχουμε αναγνωρίσει ακριβώς τον αριθμό αυτόν.
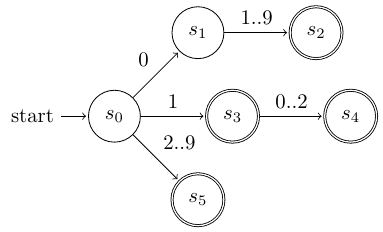
Αυτόματο πεπερασμένων καταστάσεων για αναγνώριση αριθμού μήνα¶
Αυτόματα με loops¶
Ένα αυτόματο πεπερασμένων καταστάσεων μπορεί να αναγνωρίσει ακολουθίες χαρακτήρων με απεριόριστο μήκος. Αυτό επιτυγχάνεται με τη χρήση loops στις ακμές του αυτομάτου. Δείτε για παράδειγμα το αυτόματο που ακολουθεί, το οποίο αναγνωρίζει ακολουθίες ψηφίων 0..9 οποιουδήποτε μήκους:

Αυτόματο πεπερασμένων καταστάσεων για αναγνώριση σειράς ψηφίων¶
Μια πολύ σημαντική ιδιότητα του ντετερμινιστικού αυτομάτου πεπερασμένων καταστάσεων είναι ότι η χρονική πολυπλοκότητα (και η απόδοση) της διαδικασίας αναγνώρισης δεν εξαρτάται από το μέγεθος του αυτομάτου (αριθμό καταστάσεων) αλλά μόνο από το μέγεθος του κειμένου εισόδου:
Για μέγεθος εισόδου \(S\) η πολυπλοκότητα του αυτομάτου είναι \(\mathcal{O}(S)\), ανεξάρτητα από τον αριθμό των καταστάσεων του αυτομάτου.
Αυτό εξηγείται αν σκεφτούμε ότι για κάθε ένα νέο χαρακτήρα εισόδου κατά τη διάρκεια αναγνώρισης, το αυτόματο θα κάνει το πολύ μία μετάβαση (αν η μετάβαση είναι εφικτή).
Πίνακας μεταβάσεων¶
Το αυτόματο πεπερασμένων καταστάσεων είναι μια θεωρητική μορφή. Για να υλοποιηθεί σε κάποια γλώσσα προγραμματισμού χρειαζόμαστε μια πιο συγκεκριμένη (concrete) μορφή. Ως ενδιάμεσο βήμα, μπορούμε να εκφράσουμε το αυτόματο με έναν πίνακα δύο διαστάσεων. Για παράδειγμα, ο πίνακας για το αυτόματο που αναγνωρίζει τα long, term, test είναι ο εξής:
l |
o |
n |
g |
t |
e |
r |
m |
s |
|
|---|---|---|---|---|---|---|---|---|---|
s0 |
s2 |
s1 |
|||||||
s1 |
s3 |
||||||||
s2 |
s8 |
||||||||
s3 |
s6 |
s4 |
|||||||
s4 |
s5 |
||||||||
s5* |
|||||||||
s6 |
s7 |
||||||||
s7* |
|||||||||
s8 |
s9 |
||||||||
s9 |
s10 |
||||||||
s10* |
Όπως φαίνεται στο σχήμα, ο πίνακας έχει στις γραμμές του τις καταστάσεις του αυτομάτου και στις στήλες του τους αναμενόμενους χαρακτήρες εισόδου (το αλφάβητο του αυτομάτου). Οι τερματικές καταστάσεις σημειώνονται με το *. Στην πρώτη γραμμή του πίνακα τοποθετείται η αρχική κατάσταση \(s_0\).
Στη διασταύρωση γραμμής-στήλης τοποθετούμε τη νέα κατάσταση που μεταβαίνουμε.
Αν το κελί είναι άδειο, δεν υπάρχει μετάβαση από την τρέχουσα κατάσταση με τον δεδομένο χαρακτήρα εισόδου. Συνεπώς προκύπτει σφάλμα.
Ερωτήσεις¶
Λεκτικός αναλυτής για τη γλώσσα C δέχεται ως είσοδο το string
k ; int. Τι πρέπει να επιστρέψει;
Θα απορρίψει τους χαρακτήρες εισόδου μέχρι και το
;και θα επιστρέψει μόνο τοKEYWORD_INT.Θα δημιουργηθεί σφάλμα, διότι δεν πρόκειται για έγκυρη σύνταξη της C.
Θα επιστρέψει τα σύμβολα
IDENTIFIER,SEMICOLON,KEYWORD_INT.
Σας δίνεται το αυτόματο του επόμενου σχήματος, το οποίο αναγνωρίζει διψήφιους αριθμούς από το
00έως το19για να το αξιολογήσετε. Τι λέτε;
Το αυτόματο δεν αναγνωρίζει το ζητούμενο σχέδιο (pattern).
Το αυτόματο είναι εν μέρει λάθος. Οι καταστάσεις \(s_1\), \(s_3\) πρέπει να συγχωνευτούν σε μία. Το ίδιο και οι καταστάσεις \(s_2\), \(s_4\).
Το αυτόματο είναι σωστό. Θα μπορούσε να γραφεί πιο κομψά με συγχωνεύσεις καταστάσεων αλλά αυτό δεν έχει σημασία στην απόδοση.
Γιατί στον πίνακα μεταβάσεων του παραδείγματος long, term, test οι γραμμές των τερματικών καταστάσεων είναι κενές;
Αυτό συμβαίνει πάντα με τις τερματικές καταστάσεις γιατί η αναγνώριση σταματά στο σημείο εκείνο.
Επειδή δεν υπάρχουν εξερχόμενες μεταβάσεις από τις καταστάσεις αποδοχής του συγκεκριμένου παραδείγματος.
Επειδή όταν βρισκόμαστε σε κατάσταση αποδοχής, για κάθε επόμενο χαρακτήρα προκύπτει σφάλμα.
Στον ίδιο πίνακα μεταβάσεων μπορεί μια γραμμή να έχει δύο η περισσότερα κελιά συμπληρωμένα;
Ναι. Αυτό σημαίνει ότι από την τρέχουσα κατάσταση υπάρχουν πολλαπλές μεταβάσεις, ανάλογα με την εμφάνιση διαφορετικών χαρακτήρων εισόδου.
Ναι. Αυτό σημαίνει ότι από την τρέχουσα κατάσταση μεταβαίνουμε σε μια μοναδική δεύτερη κατάσταση, με πολλούς διαφορετικούς χαρακτήρες εισόδου.
Όχι. Αυτό θα σήμαινε ότι με τον ίδιο χαρακτήρα μεταβαίνουμε σε διαφορετικές καταστάσεις.
Σχεδιάστε τον πίνακα μεταβάσεων για το αυτόματο αναγνώρισης ψηφίων.
